Tag: Big O Notation

Sometimes, solving a problem isn’t the main issue. Problems can have many different solutions and we as developers need to fine the best solution. But what makes a solution better against others? The answer can vary. However, when we write an algorithm we will try to find the solution that solves the problem faster (time), and the one that uses less resources (memory).

Time complexity

Time complexity represents the time or memory that an algorithm takes in order to complete the solution. The less time an algorithm takes, the happier our end users will be. So, knowing how to write more efficient algorithms is crucial for having better performance in our software.

How do we go about analyzing which solutions are most efficient?

Big O Notation

We can represent time complexity with math, here is when Big O Notation come to play. This notation is just a way of analyzing how long an algorithm with a given number of inputs (n) will take to complete its task.

Here are some simple time complexities with its Big O Notation, feel free to look in Wikipedia for more in-depth definitions:

O(1) Constant time: It doesn’t matter the n number of elements in our data. It will just take a single step for complete the task. A clear example is the access of an item into an array

const fruits = ["apple", "pineapple", "orange"];

// The time for getting the last item will be
// the same than getting the first item.

console.log(fruits[0]);
console.log(fruits[2]);

O(s) Linear runtime: Everything will depends on the value of s. The bigger s is, the more time it will take to resolve the algorithm. A for loop could be an example. The loop will take s number of iterations to get out of the loop.

for(let i; i < s; i++) {
   console.log(i);
}

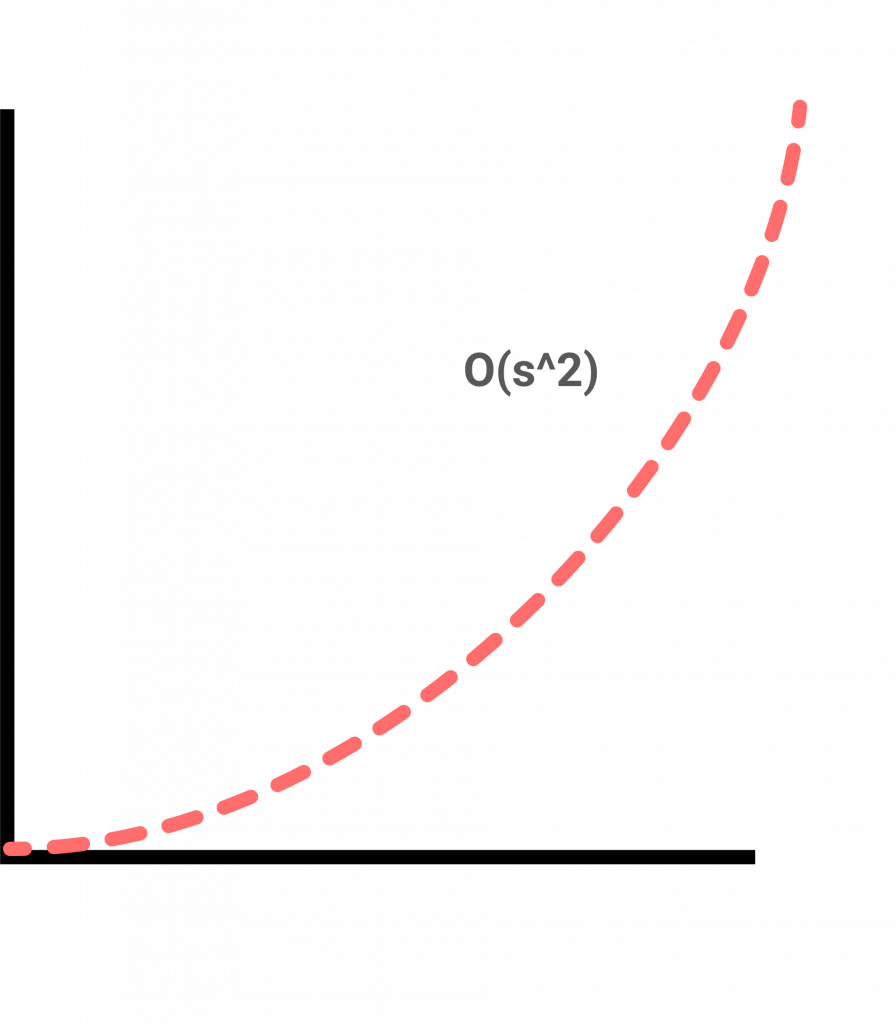
O(s2) Quadratic time: It is really common on algorithms that involve nested iterations. Giving n size, it will take square n to complete the task.

for(let i; i < s; i++) {
  for(let j; j < s; j++) {
      console.log(`${i}, ${j}`);
  }
}

O(log n) Logarithmic time: Given an input of size n, the number of steps it takes to accomplish the task are decreased by some factor with each step. For example, a binary search could be logarithmic since with every step we reduce the possible solutions in half, so the more iterations the closest we are for completing the task.

Conclusion

Time complexity and Big O Notation will help us to understand an a more visible way if an algorithm is faster or not. Different data structures have different running time. So, understanding this topics will allow us to use data structures that can fit well for a better performance.

We won’t cover all time complexities. However, I hope this short post gives you an idea of what time complexity is and how to represent those running times with math (Big O Notation).