Tag: Binary Search

This is probably one of the most useful search algorithms you will use when solving computer science problems. I’ll try to explain this search method the best I can.

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array.

Wikipedia

When searching in an array with Binary Search we need to make sure that the array is sorted, you will see why in a moment.

Linear search

Let’s create a really simple scenario, let’s pretend I give you this array:

Then I ask you to find if this array has the number 90. A linear search approach would loop through the array and check if the current item is indeed our target value, in this case the number 90. JavaScript code would look alike this:

const items = [2, 9, 13, 53, 89, 90, 98];

const findElement = search => {
   for(let i = 0; i < items.length; i++) {
      if (items[i] == search) {
         return true;
      }
   }
   return false;
}

console.log(findElement(90));

Worst case scenario would be O(N) because if the element you want to find is the last one, you will loop on the entire array.

This isn’t optimal for a sorted array, binary search time complexity is O(Log N) which is normally a better option when we threat with large data sets.

Binary search approach

For this algorithm we will need 3 pointers:

• L: Left pointer
• R: Right pointer
• M: Middle pointer

Graphically this would look like this:

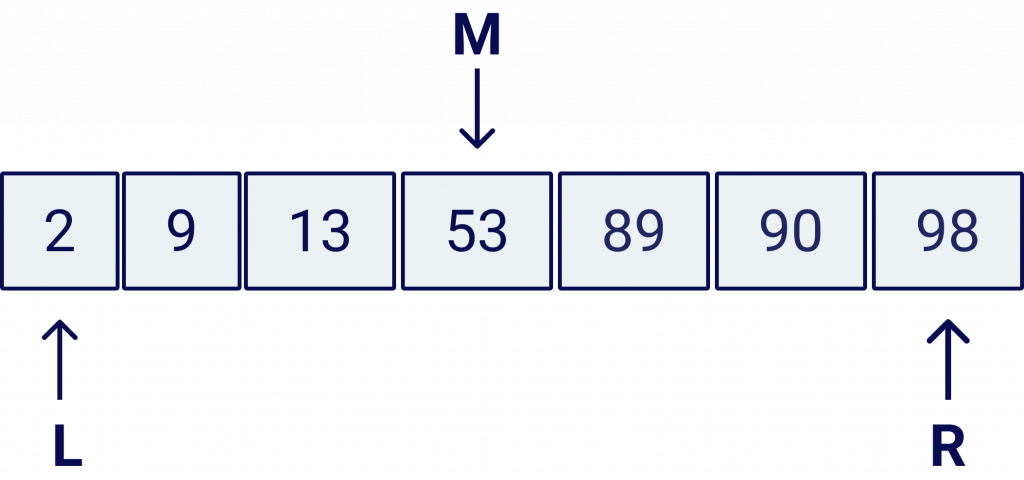
The algorithm goes like this:

• Start L pointing to the first element of the array.
• Start R pointing to the last item.
• Start a while loop until L <= R.
• Everything inside this loop will be repeated each time:
  • Start M pointing to the greatest middle value (floor) between L and R.
  • Check if the element in M position is the one you a looking for. If so, return the value.
  • At this point we need to discard one half of the array, basically chop it from the M position. We can decide which side by either converting L = M + 1 or R = M - 1. This will depends on if the element is being pointed by M is greater or lower than our target value.
• If L <= R the loop will end and it will mean that our target value is not in the array.

Code:

const items = [2, 9, 13, 53, 89, 90, 98];

const searchBinary = (elements, search) => {
  let L = 0;
  const n = elements.length;
  let R = n - 1;

  while(L <= R) {
    let M = Math.floor((L + R) / 2);
    if (elements[M] === search) return M;
    if (elements[M] < search) {
       L = M + 1;
    } else {
      R = M - 1;
    }
  }
  return -1;
}

console.log(searchBinary(items, 89));

Here is a little animation of how this algorithm would work:

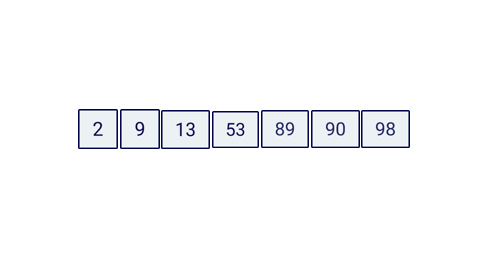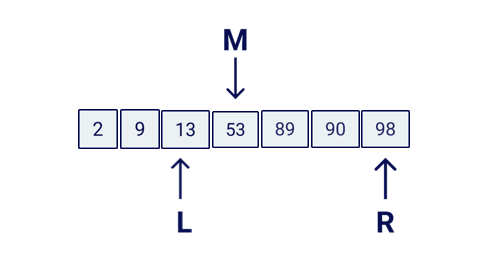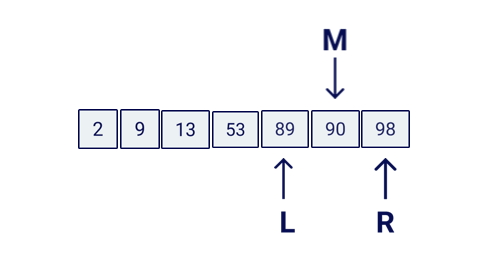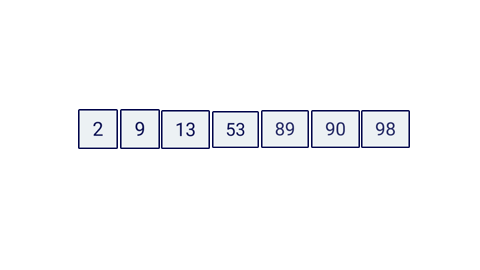
Special cases

What if there are duplicated values in our array? The previous approach will still works. However, it will only respond to the question “Is there any 90 in the array?” but what if you need the leftmost value, or the rightmost value. See the next example so you can visualize the issue with our first approach:

Leftmost

See how in the next animation, M starts in target value, but with this approach we will need to wait until L and R crosses, so it doesn’t matter if M is already in one of the target values..

Let’s tweak a little bit our current code so we can find the leftmost element.

const items = [2, 9, 13, 53, 89, 90, 90, 98, 100, 102];

const binarySearchLeftMost = (elements, search) => {
  let L = 0;
  const n = elements.length;
  let R = n;

  while (L < R) {
    M = Math.floor((L + R) / 2);
    if (elements[M] < search) {
      L = M + 1;
    } else {
      R = M;
    }
  }
  return L;
}

console.log(binarySearchLeftMost(items, 90));

Rightmost

Very similar to leftmost, we need need to chop all the right duplicated values right away, then start moving L closer and closer to R.

const items = [2, 9, 13, 53, 89, 90, 90, 98, 100, 102];

const binarySearchRightMost = (elements, search) => {
  let L = 0;
  const n = elements.length;
  let R = n;
  while (L < R) {
    M = Math.floor((L + R) / 2);
    if (elements[M] > search) {
      R = M;
    } else {
      L = M + 1;
    }
  }
  return L;
}

console.log(binarySearchRightMost(items, 90));

Conclusion

Binary search is a great algorithm for searching through a sorted array, we can either verify if an element is within the array, find the first occurrence or the last occurrence.

I hope you enjoyed and learned from this post, if you have any question let ping me on my twitter @jorgechavz